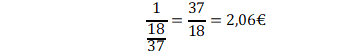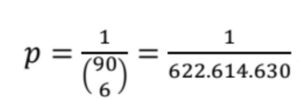L’angolo matematico di Stefano Leonesi: Superenalotto, Fulmini e Asteroidi…

In principio era un gioco: dadi e strani ossi

Il termine azzardo deriva dall’arabo al zhar (dado) e accomuna tutti quei giochi – dadi, roulette, Superenalotto, Gratta e Vinci… – il cui esito è in mano alla sorte. E’ noto che, già nel quarto millennio prima di Cristo, in Mesopotamia si giocava con una versione primitiva di dado, detta astragalo, un osso della zampa di pecora o di capra, di forma pressappoco cubica, ma più allungata.

Gli antichi dadi: ossi di astragalo

Anche i Greci e i Romani erano soliti giocare lanciando quattro astragali insieme; il miglior risultato, detto “colpo di Venere”, si verificava quando uscivano quattro facce – tra quelle allungate – tutte diverse tra loro. Già Cicerone (106 a.C. – 43 a.C.) nel De Divinatione si domandava “Cosa c’è di più incerto del lancio dei dadi? (…) dobbiamo essere così stolti da affermare che è accaduto per volontà di Venere, piuttosto che per caso?”.

Vaso che ritrae Achille e Aiace intenti a giocare a dadi, Exekias (530 a.C. circa), Musei Vaticani

Caso o Provvidenza?

Per secoli l’uomo ha continuato a inventare giochi legati alla fortuna e al caso, a divertirsi e purtroppo anche a rovinarsi con essi. Proprio il desiderio di giocare e soprattutto vincere ha stimolato lo sviluppo di un approccio razionale e matematico ai giochi, al fine di stimarne correttamente i rischi.

Tale processo è stato, in verità, assai lento fino al Medio Evo, epoca in cui il pensiero dominante del cristianesimo non lasciava spazio alla casualità degli eventi, ma solo alla provvidenza divina, che tutto controlla e decide. Durante il Rinascimento, però, illustri matematici e fisici affrontarono con maggior vigore il tema dell’incertezza: citiamo tra gli altri Luca Pacioli (ca. 1445 – ca. 1514), Gerolamo Cardano (1501-1576) e Galileo Galilei (1564 -1642); quest’ultimo nel trattato Sopra le scoperte dei dadi del 1596 affronta un problema sul lancio di tre dadi postogli dal Granduca di Toscana. Ma il loro interesse era ancora sporadico e frammentario.

Il cavaliere e il matematico

La nascita ufficiale della matematica dell’incerto o, come la chiamiamo in termini ufficiali, del calcolo delle probabilità si può collocare nel 1654, anno in cui il Cavaliere de Meré, incallito giocatore d’azzardo, pose all’amico e famoso matematico Blaise Pascal (1623-1662) alcuni problemi sul gioco dei dadi.

Blaise Pascal (1623-1662)

In particolare il Cavaliere si domandava se fosse più probabile ottenere almeno un 6 lanciando quattro volte un dado o almeno due 6 lanciando ventiquattro volte due dadi. Infatti con il primo gioco aveva accumulato una ingente fortuna, che però rischiava di perdere senza capirne il perché scommettendo sulla seconda modalità. Pascal non solo risolse il problema dell’amico, dimostrando la maggiore facilità di uscita del primo evento, ma nel farlo pose le basi al moderno calcolo delle probabilità, inteso come insieme di leggi matematiche adatte a valutare le possibilità che un evento aleatorio ha di accadere. A ciò contribuì non poco anche un altro famoso matematico dell’epoca, Pierre de Fermat (1601-1665), con cui Pascal instaurò una intensa corrispondenza epistolare sin dai tempi del Cavaliere de Meré.

Non solo giochi: operare, investire, assicurare

Dal XVIII secolo i contributi alla nuova scienza delle probabilità furono sempre più numerosi e profondi, cogliendo legami inaspettati e possibili applicazioni ai più svariati settori. Oggi, ad esempio, per una compagnia di assicurazioni sarebbe impensabile stipulare dei contratti senza aver stimato con precisione l’entità del rischio dell’evento assicurato. Lo stesso vale per le società di investimento finanziario o per le equipe mediche quando devono stabilire se operare o meno, e in tutte quelle occasioni in cui si devono prendere decisioni razionali in condizioni di incertezza.

Come sfidare la dea bendata

Torniamo ora all’aspetto più ludico della questione e domandiamoci anzitutto se conviene giocare d’azzardo e sfidare la sorte e, se sì, quale è il gioco più conveniente, favorevole e “giusto” su cui puntare? In verità, nel calcolo delle probabilità più che di “giustizia” si parla di “equità”.

Giochi equi

Si può ragionevolmente definire “equo” un gioco in cui il rapporto tra la “posta in gioco” – cioè la somma puntata – e la vincita che ne deriverebbe è pari al rapporto tra i casi favorevoli e tutti quelli possibili, ovvero alla probabilità di vittoria secondo la concezione classica; in formule:

Formula del gioco “equo”

In altre parole,

Facciamo un esempio. Nel gioco dei dadi, lanciandone uno (non truccato!), se si scommettesse 1€ sull’uscita della faccia 4 (1 caso su 6), per equità, in caso di uscita del 4 si dovrebbero incassare 6€, cioè proprio 1/(1/6)=1*6=6€. In tutti gli altri casi il gioco sarebbe sbilanciato a favore del giocatore o del “banco”, ovvero di colui che accetta le scommesse.

La definizione di gioco equo appena ricordata appare intuitivamente ragionevole e in linea col principio che quanto più bassa è la probabilità di “azzeccarci” tanto più alta deve essere la vincita (a parità di puntata).

Si noti che se un gioco è equo, non significa che ogni serata dedicata all’azzardo attraverso questo gioco si risolverà in un pareggio, ma che alla lunga, le somme vinte tenderanno a compensare quelle perse. Ma cosa significa “alla lunga”? In parole povere significa avere a disposizione infiniti soldi, infinito tempo e infinite giocate a disposizione, ipotesi ovviamente irrealizzabili nella pratica.

L’amletica scelta tra Roulette, Lotto, Superenalotto o… ?

Chiariamo subito che tutti i giochi gestiti da un “banco”, ovvero da una figura che acquisisce le poste giocate, stabilendo (naturalmente a proprio vantaggio) le relative quote da assegnare allo scommettitore in caso di vincita, non sono equi, bensì intenzionalmente e matematicamente organizzati allo scopo di far guadagnare alla lunga il banco. Tra questi ricordiamo ancora la roulette, il Lotto, il Superenalotto, i Gratta e Vinci, le lotterie in genere eccetera. Semmai possiamo evidenziare che alcuni giochi sono ancora meno equi di altri. Il Lotto, ad esempio, è assai più iniquo della roulette. Vediamone i dettagli.

La roulette “europea”

La roulette europea ha nello “zero” di colore verde il motivo di ingiustizia poiché se ad esempio puntassimo 1€ su uno specifico numero, vinceremmo 36€, mentre sarebbe giusto vincerne 37, oppure se decidessimo di puntare 1€ sul rosso, riceveremmo 2€ mentre ne dovremmo ricevere

poca differenza, vero, rispetto a 2€, ma quel tanto che basta per far pendere alla lunga la bilancia delle vincite a favore del banco. E comunque nella roulette americana si è pensato bene di inserire anche il doppio zero verde per rendere ancor più favorevole per il banco il gioco nei casinò. Sta di fatto che rispetto al Lotto e al Superenalotto la roulette rappresenta addirittura un gioco degno di lode per la sua “quasi imparzialità”. Basta infatti dare un’occhiata alla tabella N. 1 per rendervi conto di quanto nel gioco del Lotto lo Stato si comporti in modo davvero avido nei confronti dei cittadini giocatori. La tabella è compilata tenendo conto delle probabilità e della formula del gioco equo prima riportata.

Combinazioni del Lotto	Numero delle “poste” che sarebbe equo pagare	Numero delle “poste” pagate (cui togliere la tassa dell’8% sopra i 500€)
Estratto Semplice	18	11,23
Ambo	400	250
Terno	11.748	4.500
Quaterna	511.038	120.000
Cinquina	43.949.268	6.000.000

Tabella N. 1 – Quote di pagamento reali in confronto a quelle eque

La tabella 1 mostra ad esempio che in caso si indovini un singolo numero sui 5 puntati (estratto semplice) sarebbe giusto vincere 18 volte la somma puntata, mentre in realtà si vincono solo 11,23 volte la posta, senza contare che sopra i 500€ la vincita viene tassata di un ulteriore 8%. Pensate poi che in caso della fortunata “cinquina secca” lo Stato dovrebbe pagare oltre 7 volte in più rispetto a quello che invece è disposto a dare: più di 44 milioni di euro invece dei 6 milioni di euro meno le tasse.

E non è che la situazioni migliori con il tanto decantato Superenalotto, nonostante sia sempre oculatamente in prima pagina nel caso di vincite milionarie, proprio per invogliarci a giocare. Qui le valutazioni probabilistiche sono un po’ più complesse rispetto a quelle del Lotto poiché il premio è legato anche alla ripartizione di un monte premi variabile di volta in volta tra i vari vincitori delle diverse combinazioni vincenti. Ma solo per dare un’idea mostriamo che la probabilità p di vincere il jackpot, cioè indovinare tutti e 6 i numeri estratti sui 6 puntati, è pari a:

ovvero a meno di una su 600 milioni!

Da qui si capisce che, anche giocando un solo euro, le vincite in caso di jackpot dovrebbero essere superiori ai 600 milioni di euro, quindi ben più alte di quelle pur milionarie che capitano di tanto in tanto. E non dimentichiamoci che la tassazione applicata alle vincite del Superenalotto è addirittura del 20% al di sopra dei 500€.

Fulmini, asteroidi e… Superenalotto

Tanto per rendersi conto della microscopica probabilità di fare 6 al Superenalotto, si consideri che la probabilità di venire colpiti da un fulmine (senza necessariamente morire) nel corso della vita è pari a 1 su 15.300, secondo i dati del National Weather Service statunitense per gli anni 2009-2018: in pratica c’è una probabilità 40.000 volte superiore di venire prima o poi folgorati da un fulmine piuttosto che vincere il jackpot puntando una sestina secca!

Non vi basta questo? Se volete un altro metro di paragone, pensate che, secondo i dati dell’Earth Impact Monitoring del Center for Near Earth Object Studies della Nasa, la probabilità che l’asteroide “2005 ED224” colpisca la terra l’11 marzo 2030 è di circa 100 volte superiore a quella che si ha di vincere il jackpot.

In definitiva, se ritenete assai remota la probabilità di finire fulminati o che un grande asteroide impatti sulla terra nel 2030, per coerenza dovreste rendervi conto che quasi sicuramente non “sbancherete” mai il Superenalotto.

Ricette vincenti

Ma esistono dei metodi matematicamente certi per “sbancare” gli usuali giochi d’azzardo? Diciamo che sono noti da tempo dei sistemi, però puramente teorici, per vincere alla lunga con sicurezza; ricordiamo qui quello cosiddetto “della martingala” o del raddoppio, tutt’ora usato di frequente per esempio nella roulette per le puntate semplici, come “rosso o nero”. Il metodo consiste nel raddoppiare ogni volta la scommessa fino a quando non si vince, recuperando così le perdite precedenti. Poniamo il caso di puntare 1€ e perdere, allora ritentiamo puntando 2€ in modo da recuperare la perdita precedente e vincere 1€; in caso di perdita, scommettiamo 4€ in maniera da recuperare i 3€ persi fini lì e tornare a vincere 1€, e così via.

Il problema è che le somme da investire crescono esponenzialmente in modo vertiginoso e che per far funzionare il meccanismo è necessario che il banco non ponga alcun limite alle scommesse e che il giocatore disponga di infinito denaro, ma entrambe le condizioni sono purtroppo clamorosamente false. Non a caso questo sistema viene definito anche come la “rovina del giocatore” perché le perdite possono essere spaventosamente alte nei casi più sfortunati sino a ridurre sul lastrico lo scommettitore.

Tornando alla domanda iniziale, la matematica può aiutarci a vincere o almeno ad aumentare la probabilità di vittoria? Purtroppo no, almeno se vogliamo che ciò avvenga senza trucchi e inganni. La matematica può solo quantificare con precisione il livello di iniquità dei vari giochi e rendere consapevole lo scommettitore di quello a cui va incontro.

In definitiva il metodo matematicamente più ragionevole ed efficace per non perdere ai giochi d’azzardo rimane quello…. di non giocare!

Un tentativo di morale

Alla fine del nostro percorso non vogliamo passare per “bacchettoni” e fautori di una sorta di neo-proibizionismo. Molti altri svaghi e passioni (tutti?) possono diventare dannosi in caso di abuso, dal cibo all’alcol, dallo sport al sesso, dal gaming ai social network, producendo dipendenza. Anche il gioco d’azzardo, se preso con le pinze, a piccole dosi, con lucidità e consapevolezza, può regalare un sano divertimento per una sera, capace di appagare al pari di una buona cena o di una serata danzante. Magari sarebbe opportuno pianificare prima il budget sacrificabile e non superarlo in alcun caso per rifarsi delle perdite, tutt’altro che improbabili. Ma se pensiamo di non essere sufficientemente equilibrati e razionali, di avere un’indole incline a vizi e dipendenze, be’, meglio starne alla larga poiché il passo per finire nelle tenaglie della ludopatia è breve.

Dopo tutto, anche giocare al Superenalotto può avere un senso, nonostante quanto si è detto prima, ma a patto ci si investano somme minuscole, con la consapevolezza di perderle in modo quasi certo, quale pegno da pagare per godere temporaneamente dell’adrenalina di un remotissimo miraggio milionario.

Stefano Leonesi

Stampa questo articolo