Nel 1916 la ditta Watts Brothers Tool Works distribuì un volantino pubblicitario nel quale sorprendentemente si annunciava:
“Abbiamo udito di chiavi inglesi sinistrorse, vasche da bagno in pelliccia, pettini per calvi. Abbiamo giudicato ridicole tali cose e non avremmo mai creduto che potesse accadere una cosa del genere: ma ecco ora un attrezzo che fa i fori quadrati!”.
Quello che il volantino non svelava era che il meccanismo sfruttava delle proprietà geometriche di una particolare curva, e che dunque traeva piena ispirazione dalla matematica. Ma come può la matematica essere utile per praticare dei fori e soprattutto dei fori quadrati? Il nostro breve viaggio all’interno della geometria degli insiemi convessi di ampiezza costante ci permetterà di rispondere a questa domanda apparentemente bizzarra e paradossale.
Ampiezze costanti
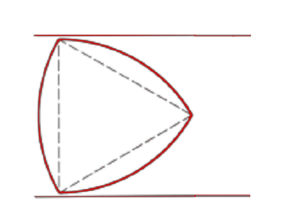
Se consideriamo un cerchio e lo facciamo rotolare tra due linee parallele poste a una distanza pari alla lunghezza del diametro del cerchio, notiamo che quest’ultimo manterrà sempre dei punti di contatto con entrambe.
Si dice anche che il cerchio è una curva a spessore o ampiezza costante, con ampiezza pari al suo diametro. Ma per quanto a prima vista possa sembrare strano, non è l’unico a godere di questa peculiare proprietà, tutt’altro. Esistono infinite altre curve capaci di rotolare all’interno di due linee parallele poste a distanza prefissata, toccandole entrambe, istante per istante. In altre parole ci sono infinite altre curve di ampiezza costante. Il primo a studiare in maniera specifica molte delle proprietà delle curve ad ampiezza costante fu, nel XVIII secolo, il grande matematico Leonhard Euler, in Italia meglio noto con il nome latinizzato di Eulero (1707-1783).
Cerchiamo ora di approfondire questa porzione della geometria meno nota specialmente ai non matematici.
Un triangolo stravagante
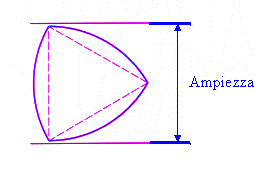
Dopo il cerchio, la più semplice curva ad ampiezza costante è senza dubbio il cosiddetto Triangolo di Reuleaux, mostrato nella figura seguente.
Questo strano “triangolo” deve il suo nome all’ingegnere e matematico tedesco Franz Reuleaux (1829-1905), docente del Politecnico di Zurigo e della Scuola Tecnica Superiore di Berlino, che per primo ne studiò caratteristiche e possibili applicazioni pratiche.
In realtà, come si è potuto notare, il triangolo di Reuleaux è un triangolo curvilineare, cioè con i lati costituiti non da segmenti retti, bensì da curve; in particolare i suoi lati sono costituiti da archi di circonferenza. Vediamo dunque come generare un triangolo di Reuleaux: si prende un triangolo equilatero e si tracciano tre archi di circonferenza aventi raggio uguale alla lunghezza del lato del triangolo con centro in ciascuno dei vertici ed estremi negli altri due. In altri termini il triangolo di Reuleaux è l’intersezione dei tre cerchi centrati nei vertici del triangolo equilatero.
Proprio per come è costruito, questo strano triangolo ha un’ampiezza costante pari alla lunghezza del lato del triangolo equilatero di partenza.
Quindi, come il cerchio, esso è capace di rotolare tra due linee parallele, mantenendo sempre dei punti di contatto con entrambe.
Poligoni di Reuleaux
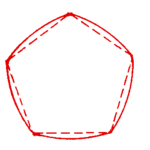
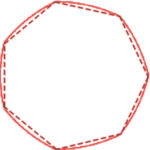
È possibile generare un numero infinito di poligoni di Reuleaux ad ampiezza costante partendo, anziché proprio dal triangolo equilatero, da un qualunque poligono regolare convesso con un numero dispari di lati. Le figure così ottenute sono delimitate da tanti archi di circonferenza, aventi lo stesso raggio, pari alla diagonale, quanti sono i vertici del poligono di partenza.
Se proviamo a calcolare il perimetro del triangolo di Reuleaux di ampiezza costante d, ci si rende conto che è dato dalla somma delle lunghezze di tre archi, ciascuno sottendente un angolo di 60°, di una circonferenza di raggio d. Ciascuno degli archi è quindi lungo 1/6 della circonferenza di raggio d, pertanto il perimetro del triangolo di Reuleaux è pari a ![]()
Sorprendentemente la formula è analoga a quella che tutti conosciamo per calcolare la lunghezza di una circonferenza di diametro (cioè ampiezza) d. In realtà Joseph Emile Barbier (1839-1889) dimostrò che il precedente risultato ha un carattere del tutto generale e dunque che ogni curva di ampiezza costante d ha perimetro ![]()
Inoltre si può osservare che, a parità di ampiezza d, il triangolo di Reuleaux ha area minore del cerchio; infatti la misura della sua superficie può essere agevolmente calcolata considerando l’area dei tre settori circolari di ampiezza pari a 60°, appartenenti ad un cerchio di raggio d e togliendo ad essa due volte l’area del triangolo equilatero generatore: ![]()
D’altro canto l’area di un cerchio di diametro d è pari a ![]()
con una maggiorazione di più del 10% rispetto all’area del triangolo di Reuleaux avente lo stesso spessore. In realtà, il matematico Henri Lebesgue nel 1914 ha dimostrato che queste due figure costituiscono proprio gli “estremi opposti” della famiglia di curve piane di ampiezza costante, nel senso che tra tutti i convessi piani di ampiezza costante fissata, il triangolo di Reuleaux è l’unico insieme di area minima ed il cerchio è l’unico insieme di area massima.
Facciamoli ruotare
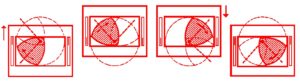
Facendo ruotare o rotolare dei poligoni di Reuleaux ci si accorge di quali sorprendenti e bizzarre proprietà essi godano. Ad esempio ognuno è in grado di ruotare all’interno di un quadrato avente il lato di lunghezza pari alla sua ampiezza, toccando sempre contemporaneamente i quattro lati del quadrilatero. Analizziamo nei dettagli il caso del triangolo di Reuleaux. Durante il movimento, il triangolo è in grado di spazzare la maggior parte dell’area del quadrato, fatta eccezione per delle piccole zone vicine ai quattro vertici. Più precisamente, l’inviluppo del triangolo di Reuleaux in movimento all’interno del quadrato segue un andamento ellittico in prossimità dei vertici. Le ellissi in oggetto sono centrate nei vertici opposti agli arrotondamenti ed hanno assi ruotati di 45 gradi rispetto ai lati del quadrato (vedi figura 7).
Se ad esempio prendiamo un triangolo di Reuleax di spessore 1, troveremo che l’area da esso spazzata corrisponde a 0,98770039…, una misura di quasi il 99% dell’area del quadrato circoscritto. C’è comunque da notare che il centro di rotazione del triangolo di Reuleaux in movimento all’interno di un quadrato non rimane fisso, e neppure si muove descrivendo una traiettoria circolare, come un primo e superficiale approccio potrebbe far pensare. S. Wagon ha dimostrato che il suo percorso è costituito dalla composizione di quattro archi di ellisse, ciascuna centrata nel vertice opposto all’angolo da arrotondare e con assi ruotati di 45 gradi rispetto ai lati del quadrato.
Mostreremo ora una panoramica di alcune delle stravaganti e comunque funzionali applicazioni di natura meccanica che sfruttano le proprietà e le caratteristiche dei triangoli e in genere dei poligoni di Reuleaux.
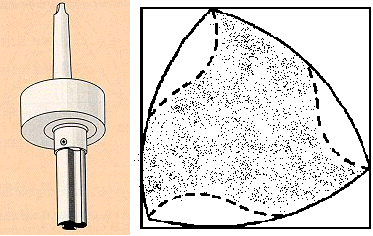
Punte sorprendenti
E’ per certi versi più sorprendente e singolare quella citata all’inizio nel titolo dell’articolo e risalente al 1914, quando un ingegnere inglese Harry S. Watts, sfruttando la capacità dei triangoli di Reuleaux di spazzare quasi completamente l’area del quadrato ad essi circoscritto, inventò una punta da trapano capace di realizzare dei fori quadrati. La sezione della punta (vedi figura 9) è un triangolo di Reuleaux con tre insenature per permettere il taglio dei bordi e la fuoriuscita dei trucioli. Abbiamo già detto che, durante la rotazione, il centro di rotazione del triangolo non rimane fisso, ma si muove tracciando una traiettoria composta da quattro archi di ellisse. È questo il motivo per il quale la cosiddetta Punta di Watts è dotata di uno speciale mandrino (vedi figura 9) che rende il tutto perfettamente funzionante.
La Punta di Watts è stata realmente prodotta nel 1916 dalla Watts Brothers Tool Works e ancora recentemente nel loro catalogo c’erano punte da trapano per fori quadrati, pentagonali, esagonali ed ottagonali.
Idranti a prova di caldo
Da circa cinquanta anni gli idranti della città di Philadelphia sono dotati di rubinetti la cui sezione è un triangolo di Reuleaux. Il motivo di tale forma è da ricercare nel tentativo di evitare facili manomissioni operate da vandali o semplicemente da cittadini accaldati che tentano di sfuggire all’afa dell’estate dell’east-coast statunitense concedendosi una doccia “di strada”. Infatti, grazie allo spessore costante del rubinetto, le comuni chiavi inglesi non fanno alcuna presa su di esso, scivolando come su di un cilindro.
Tombini economici
Alcune città del Minnesota hanno in dotazione dei tombini a forma di triangolo di Reuleaux. Come abbiamo già visto, in questo caso ci sarà un risparmio di più del 10% di materiale, e quindi di peso e costo, rispetto ai classici tombini circolari mantenendo la stessa ampiezza.
Motori rotanti
Felix Wankel (1902-1988), sebbene non abbia mai avuto la patente di guida, negli anni ’20 progettò un motore il cui pistone non ha l’usuale movimento lineare alterno, bensì rotatorio all’interno di una camera statore. La sezione del pistone del motore Wankel è proprio un triangolo di Reuleaux. Tale motore è stato effettivamente in dotazione su modelli di auto Mazda e in particolare sul modello RX7.
Tra l’altro anche alcune pompe volumetriche rotanti per acquari sono simili per concezione al motore Wankel
Monete speciali
Le monete da 20 e 50 pence inglesi sono modellate a forma di ettagoni di Reuleaux, e addirittura esiste una moneta canadese che ha la sagoma proprio di un triangolo di Reuleaux; infatti lo spessore costante di tali pecunie garantisce comunque il loro utilizzo, senza rischi di inceppamento, nei distributori automatici dotati degli usuali dispositivi di riconoscimento “a spessore”, adatti per le monete circolari.
Proiettori triangolari
In alcune macchine da proiezione cinematografica lo strumento che permette di ottenere una immagine nitida, consentendo alla pellicola di avanzare ad intermittenza, ha le sembianze di un triangolo di Reuleaux incorniciato in un quadrante rettangolare (vedi figura). La rotazione del triangolo causa lo spostamento verso l’alto del telaio chiudendo l’obiettivo fintantoché la pellicola avanza. Il proseguimento della rotazione del triangolo causa il ritorno in basso del quadrante, riaprendo l’obiettivo con la conseguente visione del fotogramma successivo. In gergo tecnico tale meccanismo è chiamato gripper.
Strane automobili
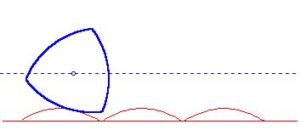
Essendo in vena di stravaganze, prendiamo in considerazione la possibilità di costruire automobili (che potremmo chiamare Reuleaux-auto) con ruote la cui sezione è rappresentata da un triangolo di Reuleaux. L’unico punto concepibile per far passare l’asse sarebbe il baricentro del triangolo, ma la difficoltà principale nasce proprio dal fatto che durante il rotolamento il baricentro non sta sempre alla stessa distanza dal bordo, ma, come abbiamo visto, compie una traiettoria formata da quattro archi di ellisse. Di conseguenza l’altezza del baricentro muterebbe continuamente e, pur avendo l’accortezza di sincronizzare le quattro ruote in maniera tale da far loro avere la stessa fase iniziale, l’auto si solleverebbe e ricadrebbe a singhiozzo, come mostrato nella figura successiva.
Si potrebbe ovviare al problema dotando i semiassi di dispositivi che permettano al baricentro di rimanere ad un’altezza fissa, e probabilmente in qualche parte del pianeta c’è qualche bizzarro inventore che ha già tradotto in realtà queste nostre singolari considerazioni. Di certo, Paul Kunkel si è preoccupato di capire quale forma dovesse avere il terreno per permettere una tranquilla gita senza sobbalzi su una normale automobile dotata però di ruote a forma di triangolo di Reuleax. Il risultato è visibile nella figura seguente.
Termina qui il nostro viaggio tra le intriganti proprietà delle curve a spessore costante le quali hanno i più degni e famosi rappresentanti nella circonferenza e nel triangolo di Reuleaux.
 Il Settempedano
Il Settempedano