Il Settempedano
Le vie matematiche della lotta per la vita
Nel 1925-26 due scienziati tentarono di spiegare le dinamiche della predazione e della lotta per l’esistenza
Primi approcci della matematica alla biologia
Era il 1798 quando l’inglese Thomas Malthus (1766-1834) – economista e pastore anglicano – propose uno studio su come varia nel tempo il numero di individui di una certa popolazione, che siano persone, animali, batteri o virus, dunque riguardante un tema quanto mai attuale come le epidemie. Egli formulò una legge deterministica sulla crescita di una qualunque popolazione isolata, cioè che non abbia scambi con l’esterno né vincoli alimentari o di altra natura, insomma che viva in un ambiente ideale e accogliente. Secondo la legge oggi detta malthusiana, la velocità di crescita è direttamente proporzionale al numero di individui della popolazione stessa. In formule noi matematici scriveremmo così:
con N numero di individui, dN/dt la sua variazione nel tempo ed r una costante di proporzionalità.
Senza addentrarci nei tecnicismi, questo può significare ad esempio che se la popolazione raddoppia, anche la sua velocità di crescita raddoppia. E la rapidità dipende dal valore della costante di proporzionalità che nel caso precedente è pari a 2. Da questa assunzione tutto sommato condivisibile ed intuitiva – più si è e più figli si fanno – discende che se la costante è positiva, la popolazione è comunque destinata ad aumentare esponenzialmente nel tempo in modo vertiginoso, se è negativa, invece, a diminuire ed estinguersi in tempi relativamente brevi, se è zero, la popolazione resta stabile.
In verità le ipotesi semplificative su cui si basa il modello di Malthus sono troppo forti: è impensabile ipotizzare che una popolazione cresca illimitatamente nel tempo senza alcun vincolo ambientale: prima o poi mancheranno spazi e risorse, nasceranno malattie ed epidemie, ci sarà carenza di cibo e magari per esso gli individui si fronteggeranno all’ultimo sangue secondo il famoso adagio latino: “mors tua vita mea”.
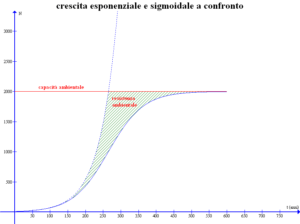
In effetti non tardò molto, per la precisione era il 1838, che il biologo belga Pierre F. Verhulst (1804-1849) introdusse una variante più realistica del modello malthusiano, sostituendo il coefficiente costante r di crescita con uno variabile che diminuisce all’aumentare del numero di individui della popolazione. Il modello tiene cioè conto che quanto più è elevato questo numero tanto peggiori diventano le condizioni di vita in un ambiente comunque dotato di risorse non illimitate: carestie, malattie, lotte fratricide per la sopravvivenza producono tassi di natalità sempre più bassi, tassi di mortalità crescenti e condizioni di vita sempre più dure. Stavolta la curva della popolazione, oggi detta curva logistica o sigmoidale, all’inizio segue ancora un andamento esponenziale, tuttavia man mano la crescita va smorzarsi sempre più corposamente fino a quando la popolazione va a stabilizzarsi su un certo livello di equilibrio che dipende dalle risorse che l’habitat mette a disposizione (capacità ambientale); si veda la figura 1.
Figura 1. Confronto tra curve maltusiana e logistica
I modelli matematici di Volterra-Lotka e il sistema preda-predatore
I tempi diventarono maturi per affrontare il più complesso studio dell’interazione tra specie differenti che coabitano in un certo ambiente e dunque per studiare quelli che in biologia vengono detti gli ecosistemi. Tra i primi a credere fortemente all’esistenza di stretti legami di mutua dipendenza tra specie conviventi fu il biologo per antonomasia Charles Darwin (1809-1882), ma i pionieristici tentativi di quantificare e modellizzare queste relazioni si devono al matematico italiano Vito Volterra (1860-1940) e al chimico austriaco-statunitense Alfred J. Lotka (1880-1949) i quali indipendentemente tra il 1925 e 1926 raggiunsero risultati analoghi.
Charles Darwin, Vito Volterra e Alfred J. Lotka
Le loro equazioni posero solide basi alla feconda applicazione della matematica alla biologia fino ai giorni nostri. Qui parleremo con malcelato patriottismo del lavoro di Volterra. Lo spunto per affrontare la questione gli venne proposto dal genero, lo zoologo Umberto D’Ancona, il quale aveva notato, con una certa sorpresa, un aumento percentuale superiore dei pesci predatori rispetto all’aumento del totale del pescato e delle prede nell’Adriatico durante e appena dopo la prima guerra mondiale. D’Ancona aveva attribuito empiricamente questo maggior incremento dei predatori all’interruzione della pesca provocata dal conflitto navale, ma auspicava motivazioni scientifiche sul fatto piuttosto contro intuitivo che l’assenza della pesca non favorisse poi così tanto i pescatori visto l’aumento percentuale dei pesci predatori. In poco tempo Volterra perfezionò un modello matematico (composto da due equazioni particolari ma relativamente semplici) in grado di descrivere la convivenza di un numero qualsiasi di specie animali in competizione fra loro in un certo ambiente. A tale modello Volterra diede il nome “Teoria matematica della lotta per la vita”. In esso si descrive una situazione del tipo preda-predatore in cui una delle due popolazioni (i predatori) ha bisogno dell’altra (le prede) per sopravvivere a scapito di quest’ultima.
Le leggi della predazione e un auspicabile equilibrio
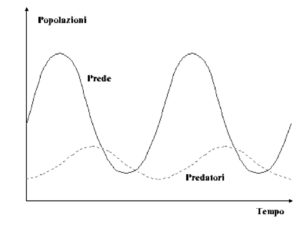
Le equazioni impostate da Volterra conducono a tre conclusioni principali da lui stesso definite “leggi”: secondo la prima legge, il numero di individui delle due popolazioni – prede e predatori – oscillano secondo andamenti ciclici tra loro leggermente sfalsati: dopo un certo tempo T ritornano ai valori di partenza (Fig.2) e riassumono lo stesso trend. La seconda afferma che le medie delle due popolazioni nel periodo T non dipendono dai valori iniziali (principio di conservazione delle medie). La terza dimostra che un abbattimento indiscriminato delle due popolazioni (come avviene nella pesca o nei trattamenti insetticidi non selettivi) causa un aumento della percentuale del numero delle prede rispetto a quella dei predatori, mentre l’assenza di un prelievo generalizzato favorisce il fenomeno contrario. Con tale legge Volterra forniva al genero d’Ancona la conferma alla sua ipotesi.
Figura 2. Ciclicità di prede e predatori prevista dalle equazioni di Volterra-Lotka
Qualche commento sulle leggi di Volterra. Il fenomeno ondulatorio previsto dalla prima legge (Fig. 2) si può spiegare ipotizzando che l’aumento delle prede comporta maggiore disponibilità di cibo per i predatori, i quali dunque prosperano e accrescono di numero; a seguito della loro crescita, però, aumenta anche il loro fabbisogno alimentare; la conseguente intensificazione dell’attività predatoria provoca un calo delle prede; di lì a poco allora anche i predatori diminuiscono per la carenza del cibo disponibile riportando il sistema alle condizioni iniziali secondo un equilibrio dinamico; quell’equilibrio intorno al quale per la seconda legge oscillano le popolazioni di prede-predatori anche cambiando le condizioni iniziali: sotto il profilo biologico, il punto di equilibrio corrisponde al valore in cui le prede generate coincidono con quelle mangiate dai predatori.
La terza legge asserisce che un soppressione indifferenziata delle due popolazioni – come nella pesca con reti a maglie piccole o a strascico, o nei trattamenti con insetticidi non selettivi (una forma di “pesca agronomica”) – determina un incremento percentuale delle prede rispetto a quella dei predatori.
Pesca selvaggia
Questo non giustifica la pesca indiscriminata, capace di condurre alla estinzione sia di prede che di predatori, piuttosto suggerisce che nella pesca come in agricoltura il ricorso a sistemi mirati quali la pesca selettiva e la lotta biologica sono ben più efficaci dell’uso di metodi invasivi come la pesca selvaggia o l’impiego di insetticidi. Ad esempio i trattamenti con insetticidi, i quali portano ad eliminare ogni tipo di insetto, sia quelli predatori sia delle loro prede, cioè degli insetti dannosi per le nostre piante, in base alla terza legge di Volterra possono condurre ad un incremento percentuale delle prede, dunque degli insetti nocivi per le colture, ottenendo un effetto controproducente.
Trattamento pesticida in agricoltura
Pensate un po’, non solo la pesca ma anche l’agricoltura danno ragione al modello matematico di Volterra-Lotka!
Ancora una volta si mette in risalto l’utilità della matematica nei più disparati campi della nostra vita, in grado come è di fornire potenti strumenti qualitativi e quantitativi, sia diagnostici che previsionali, capaci di suggerire come comportarsi e quali scelte operare per il bene nostro e dell’ambiente. Il problema è che l’Homo “sapiens” troppo spesso non ne tiene conto.
Stefano Leonesi
