L’Angolo matematico: “Terremoti… logaritmici”

Come una stravagante funzione matematica consente di misurare l’energia sprigionata dai sismi e molto altro

di Stefano Leonesi

I terremoti da sempre causano distruzioni e incutono paura. Secondo antiche credenze erano provocati dai movimenti di misteriosi giganti presenti nelle viscere della terra. Ma, al di là delle leggende, la scienza moderna ha permesso una comprensione sempre più profonda delle origini e delle dinamiche sismiche, ma non è – almeno finora – in grado di prevedere i terremoti con la necessaria accuratezza; tuttavia è capace di misurarne con precisione la “forza” attraverso opportune gradazioni di riferimento, dette scale.

Mercalli contro Richter

La Scala Mercalli fu tra le prime ad essere introdotta e prende il nome dal sacerdote sismologo Giuseppe Mercalli (1850-1914), milanese di nascita, ma napoletano di adozione visto che fu per lungo tempo docente di vulcanologia e sismologia presso l’università di Napoli, che la ideò nel 1897.

Questa scala ha la pecca di non essere oggettiva poiché si basa esclusivamente sugli effetti e sulle sensazioni che il terremoto produce – spavento, vibrazioni, danni, crolli,… -, che ovviamente dipendono non solo dall’intensità propria del sisma, ma anche dalla solidità delle costruzioni della zona interessata, dalla distanza dall’epicentro e da altro ancora. Tuttavia, senza adeguati strumenti di misura, ci si poteva basare solo su scale che tengono conto esclusivamente di tali conseguenze provocate dai terremoti su persone o cose.

Si è sentita allora l’esigenza di escogitare sistemi con cui misurare rigorosamente e in modo matematico la quantità di energia effettivamente sprigionata da un terremoto. La prima scala dotata di tali caratteristiche fu introdotta nel 1935 dal sismologo statunitense Charles Francis Richter (1900-1985) e per questo oggi chiamata Scala Richter o delle magnitudo (dal latino, a significare “grandezza”).

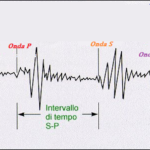
Tuttavia queste scale cosiddette oggettive, a differenza di quelle empiriche e descrittive come la Mercalli, necessitano di una fitta rette di strumenti, i sismografi (dal greco “seismós” e “graphein”, indicanti rispettivamente “terremoto” e “scrivere”), in grado di rilevare e registrare le onde sismiche su di un grafico opportuno, il sismogramma.

Sismi e logaritmi

Per la sua scala delle magnitudo, Richter decise di adoperare una particolare funzione matematica, il logaritmo decimale; più precisamente la magnitudo M è espressa dal logaritmo decimale del rapporto fra l’ampiezza massima A delle oscillazioni registrate da un particolare sismografo a torsione, detto di Wood-Anderson, e l’ampiezza Ao di un terremoto di riferimento con epicentro a 100 km (oltre ad aggiustamenti dovuti alle diverse distanze degli strumenti dall’epicentro attraverso leggi di attenuazione), in formule:

M = Log¹º (A/Ao).

Ma non vi fate spaventare. Senza entrare troppo nei tecnicismi, la precedente formula equivale a dire che 10M = A/Ao. Ciò significa che elevando 10 alla magnitudo si ottiene questo rapporto tra le ampiezze delle oscillazioni. Ad esempio, i terremoti di magnitudo M = 6 provocano oscillazioni 10 volte più grandi di quelle con magnitudo 5 e liberano un’energia di circa 32 volte superiore; così, rispetto ai sismi di magnitudo 4 generano fluttuazioni 10×10=100 volte maggiori con un aumento di energia addirittura di circa 32×32, ovvero di quasi 1000 volte. Tra l’altro esistono formule empiriche che permettono di dedurre l’energia liberata E conoscendo la magnitudo M, ad esempio per l’Italia si può usare la seguente: Log¹º E = 5 + 1,5 M.

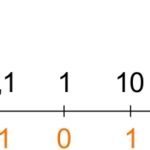
Ma qual è il motivo che spinse Richter ad utilizzare proprio una scala logaritmica? Il fatto è che le oscillazioni dei terremoti più violenti sono anche milioni di volte più ampie di quelle dei sismi più deboli; ed è proprio il logaritmo la funzione ideale e più comoda ogni qual volta si intende concentrare risultati tanto disparati in un intervallo molto piccolo di valori; si evita in tal modo il ricorso a numeri troppo grandi e disagevoli. Come accennato prima, un sisma di magnitudo 7, rispetto ad uno di magnitudo 3 produce oscillazioni di 10^(7-3) = 10^4 = 10.000 più ampie, eppure su tale scala si differenziano solo di 4 unità “logaritmiche”. Numeri positivi molto piccoli (<1) si trasformano semplicemente in valori negativi in virtù delle proprietà delle potenze. Si veda la scala logaritmica seguente per farsi un’idea migliore di come e quanto essa riesca a trasformare e concentrare range molto ampi di valori.

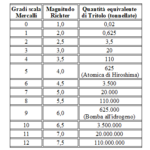
Terremoti vs Tritolo

Nella tabella seguente mettiamo approssimativamente a confronto le scale Mercalli, Richter e l’esplosivo necessario, tritolo in particolare, per ottenere effetti simili ai sismi corrispondenti.

Il sisma più devastante

Sebbene il logaritmo possa assumere teoricamente valori infinitamente grandi, sia in positivo che in negativo, per la magnitudo registrata nei terremoti le cose (per fortuna) vanno diversamente. Si pensi che il più forte terremoto dell’epoca moderna, quello che il 22 maggio del 1960 devastò il Cile, sprigionando un’energia di circa tre milioni di volte superiore a quella della bomba atomica di Hiroshima, ha fatto registrare una magnitudo stimata intorno ad “appena” 9.2-9.6: questo non significa che non sia stato catastrofico, ma solo che l’intervallo dei valori sul quale il logaritmo riesce a convogliare il range delle energie è nella pratica molto ristretto: i sismografi attualmente più sensibili non sono ad esempio in grado di registrare vibrazioni – comunque assolutamente impercettibili per l’uomo – di magnitudo inferiori a –3.

Il logaritmo: un modello di versatilità

La capacità del logaritmo di semplificare i calcoli e smorzare valori molto grandi e amplificare quelli molto piccoli viene sfruttata in molte altre circostanze, dal decadimento radioattivo usato ad esempio nel metodo di datazione dei materiali di origine organica del Carbonio-14 al pH per misurare l’acidità o la basicità di una soluzione acquosa, dall’intensità sonora espressa con i famosi decibel (dB) alla sensazione luminosa dell’occhio umano: queste e molte altre situazioni si regolano su scale logaritmiche. In altre parole, siamo tutti immersi, magari senza saperlo, in un mondo e in una natura logaritmici.

Richter, riflettendo dopo molti anni sulla sua scelta di usare il logaritmo per la sua scala delle magnitudo, ebbe una volta a dire: “Sono stato fortunato perché il logaritmo è veramente un … congegno del diavolo”.

Ma per noi matematici è “soltanto” uno tra i tanti strumenti concettuali a cui possiamo ricorrere per descrivere, modellizzare, prevedere fenomeni in modo efficiente.