Formule tra guerra e pace
Tutti sanno che con la resa del Giappone, il 2 settembre 1945, termina la sciagurata seconda guerra mondiale. Un fatto meno noto è che nel 1935 un matematico inglese, Louis Fry Richardson (1881-1953, vedi figura 1) preoccupato per la minaccia di un nuovo conflitto mondiale, presentò alla rivista Nature un articolo che, riprendendo ed ampliando un suo lavoro del 1919, descriveva in termini matematici le leggi che regolano la corsa agli armamenti e le cause e origini delle guerre.
- Figura 1 – Louis Fry Richardson (1881-1953)
Le sue equazioni, oggi note proprio come Modello di Richardson, mostravano come il disarmo unilaterale imposto alla Germania dopo la Grande Guerra del 1915-18, unito al crescente livello degli armamenti dei Paesi vincitori, avrebbe provocato inevitabilmente di lì a poco una nuova escalation militare.
Egolandia e Alterlandia
Il modello di Richardson aveva il pregio di tradurre in precise formule dei concetti sfumati e vaghi quali ostilità, bellicosità, percezione di insicurezza e rancore. Nella versione più semplice prevedeva l’esistenza di due nazioni o più in generale di due coalizioni contrapposte che egli chiamò Egolandia e Alterlandia (dal latino ego, “io”, e alter, “l’altro”). Analizzando statisticamente i dati sugli armamenti nel periodo 1909-1914, ipotizzò che le decisioni di aumentare o diminuire la corsa alle armi seguissero essenzialmente tre regole: la velocità con cui due nazioni si armano è proporzionale a quanto si sentono minacciate, è limitata dal costo sociale degli armamenti e, infine, è condizionata dai reciproci sentimenti di ostilità o amicizia sviluppatisi negli anni: quest’ultimo fattore è interpretabile come la misura dei rancori non risolti o delle consolidate cooperazioni tra le due parti. Sulla base di queste semplici regole, Richardson fu il primo a trasformare in rigorose equazioni matematiche le dinamiche che regolano i rapporti e i conflitti internazionali, permettendo di analizzarli razionalmente, di fare previsioni, simulazioni e sulla base di queste suggerire cambiamenti di rotta onde evitare sanguinosi scontri.
C’è comunque da dire che la guerra e le sue cause costituiscono un sistema assai complesso e che, come tutti i modelli matematici, anche quello di Richardson dà una rappresentazione semplificata e parziale della realtà, di per sé troppo complicata per essere tradotta dettagliatamente da equazioni facilmente risolvibili; ma è proprio grazie a queste opportune semplificazioni che tali modelli consentono di coglierne gli aspetti fondamentali, sfrondando il reale da quei dettagli meno utili ed importanti.
Corsa agli armamenti e rette di equilibrio
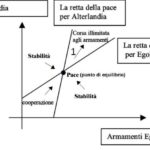
Quando nelle equazioni del modello di Richardson i fattori che inducono ad aumentare le spese militari di una nazione sono controbilanciati da quelli che spingono a ridurle, il risultato è una situazione di equilibrio, in cui il livello degli armamenti viene mantenuto costante e la propensione alla guerra sotto controllo. Questa situazione di equilibrio, nella rappresentazione grafica del modello, assume per ciascuna nazione l’aspetto di una retta su un piano cartesiano con gli assi a rappresentare il livello dei rispettivi armamenti (vedi figura 2).
- Figura 2 – Il modello matematico di Richardson, con le rette di equilibrio degli armamenti
I punti di equilibrio comuni ad entrambe le coalizioni rappresentano le condizioni di effettiva pace, in cui entrambe le parti sono soddisfatte del grado di sicurezza raggiunto, del prezzo da pagare per mantenerlo e del rispetto del loro “onore”; ma dal punto di vista geometrico questi punti comuni di stabilità altro non sono che il punto di intersezione tra le due rette di equilibrio.
Pace e stabilità
E’ naturale pensare che nel corso del tempo si possono manifestare delle perturbazioni che fanno allontanare le due nazioni da queste condizioni di equilibrio: tensioni, dissidi, scontri. Ma il modello mostra come talune perturbazioni non conducono necessariamente alla guerra, bensì vengono assorbite gradualmente: sono tali quelle che provocano senso di insicurezza solo in una delle due nazioni cosicché l’altra non alimenta il gioco al rialzo del riarmo; altre perturbazioni addirittura innescano un meccanismo virtuoso di cooperazione quando in entrambe le nazioni lo sforzo economico e sociale di sostenere la difesa con eserciti ed armamenti supera il senso di insicurezza; in pratica non si spende in armi se non ci si sente minacciati. Questi scenari suggeriscono una pace stabile, in cui le interferenze alle condizioni di equilibrio non conducono alla guerra, ma vengono appianate garantendo solide prospettive di pace: dal punto di vista grafico, la situazione ritorna verso il punto di intersezione che rappresenta la pace (le tre frecce non numerate nella figura 2).
Escalation militari e falsi miti
Altre tipologie di perturbazione, invece, vengono amplificate sempre più a testimoniare una pace instabile, dov’è elevato il rischio che alla prima occasione si scateni da ambo le fazioni una corsa illimitata agli armamenti e ci si allontani definitivamente (freccia numerata con 1 nella figura 2) dal punto di intersezione che rappresenta la pace. Non è un segreto che il circolo perverso dellla crescita reciproca degli armamenti non produce alla lunga percezioni di forza e sicurezza, ma al contrario paura e consapevolezza della forza dell’altro, favorendo il ricorso alla guerra o al collasso economico e politico di uno dei Paesi in competizione (si pensi al crollo dell’URSS durante la guerra fredda).
Prospettive matematiche della pace
In definitiva il punto essenziale che la matematica e il modello di Richardson nello specifico evidenziano non è tanto l’esistenza teorica di un punto di equilibrio, cioè di una pace possibile, ma suggerisce scientificamente come passare da condizioni di pace instabile a quelle di una pace stabile e duratura: occorre rendere più alti e sconvenienti i costi economici, sociali e ambientali che la corsa agli armamenti produce e, meglio ancora, ridurre il senso di insicurezza. Una maniera per farlo è quella di sviluppare e rafforzare gli scambi commerciali e turistici tra i Paesi, creando un clima di collaborazione e di maggiore conoscenza reciproca fra le popolazioni. Ciò diminuirà il timore e quindi, per dirla in termini matematici, porterà ad una riduzione dei coefficienti di difesa e di ostilità. Del resto, i legami economici creano interessi e convenienza al mantenimento della pace. Ma tutto questo si può codificare e modellizzare appunto in termini rigorosi e matematici, ipotizzando scenari, soluzioni e prospettive nei vari casi.
A chi gli domandava se il suo modello matematico fosse in grado di prevedere lo scoppio della prossima guerra, Richardson rispondeva:
“Le equazioni del modello sono soltanto una descrizione di cosa la gente farebbe se non si fermasse a pensare (…). Il processo descritto dalle equazioni non deve essere considerato come inevitabile. È quello che accadrebbe se all’istinto e alla tradizione fosse permesso di agire senza controllo (…)”.
Purtroppo è ciò che avvenne: di lì a poco, la Seconda guerra mondiale avrebbe fatto oltre 50 milioni di morti e provocato indicibili sofferenze e distruzioni.
E così è ancora oggi, quando bramosia e ideologie soffocano e offuscano non soltanto l’etica e lo slancio verso un bene comune, ma il pensiero razionale stesso, matematico per così dire, che suggerisce l’indiscutibile e oggettiva convenienza collettiva degli atteggiamenti cooperativi a svantaggio di quelli ostili. Ma l’uomo, purtroppo è un essere solo a tratti razionale, invero assai ingordo, manipolabile ed emotivo.
Stefano Leonesi
 Il Settempedano
Il Settempedano